PERTEMUAN 18 ( VOLUME BIDANG PUTAR DENGAN METODE CINCIN )

VOLUME BIDANG PUTAR DENGAN METODE CINCIN

Volume Benda Putar merupakan sebuah volume yang dihasilkan dari luasan yang diputar dengan poros putar tertentu (sumbu x / sumbu y). Jadi salah satu bentuk pengaplikasian integral.

Selain untuk menghitung luas di bawah kurva juga untuk menghitung volume pada benda putar.

Misal paling sederhana dari benda putar adalah tabung. Volume sebuah tabung tersebut didapatkan dari luas alas yang memiliki bentuk lingkaran yang dikalikan tinggi.

metode cincin (washer method), yaitu suatu metode yang menggunakan integral dalam menentukan volume benda putar yang memiliki lubang. Cincin dalam metode ini dibentuk oleh hasil putaran persegi panjang terhadap sumbu putaran tertentu (sumbu putaran tidak berimpit dengan sisi persegi panjang), seperti terlihat pada gambar berikut.

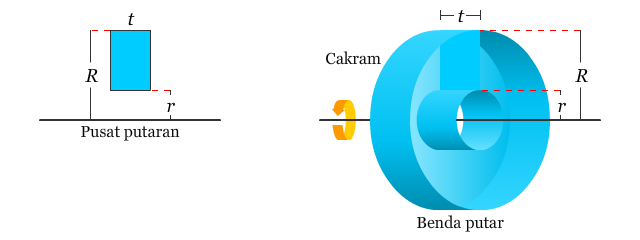
Jika r dan R secara berturut-turut merupakan jari-jari dalam dan luar dari cincin dan t merupakan ketebalan cincin, maka volumenya dapat ditentukan sebagai berikut.

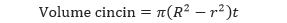
Untuk mengetahui bagaimana konsep ini dapat digunakan untuk menentukan volume benda putar, perhatikan daerah yang dibatasi oleh jari-jari luar R(x) dan jari-jari dalam r(x), seperti yang ditunjukkan gambar di bawah ini.

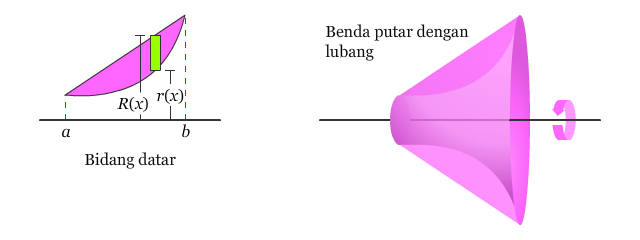
Jika daerah tersebut diputar menurut sumbu putar yang diberikan, volume benda putar yang dihasilkan adalah

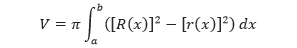
Perhatikan bahwa integral yang melibatkan jari-jari dalam merepresentasikan volume lubang yang dikurangkan dari integral yang melibatkan jari-jari luar. Untuk lebih memahami dalam menemukan volume benda putar dengan metode cincin, perhatikan contoh berikut.

Contoh: Penggunaan Metode Cincin

Tentukan volume benda putar yang dibentuk oleh putaran daerah yang dibatasi oleh grafik dari y = √x dan y = x2 terhadap sumbu-x, seperti yang ditunjukkan oleh gambar berikut.

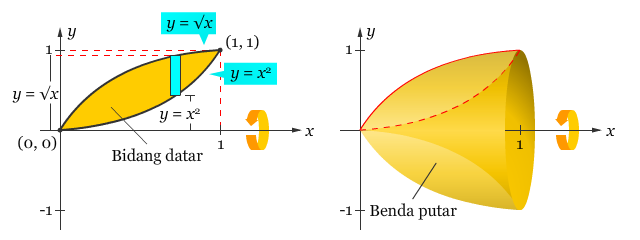
Pembahasan Dari gambar di atas dapat ditentukan bahwa jari-jari luar dan dalamnya adalah sebagai berikut.

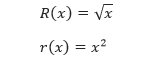
Dengan mengintegralkan dengan batas antara 0 dan 1, menghasilkan

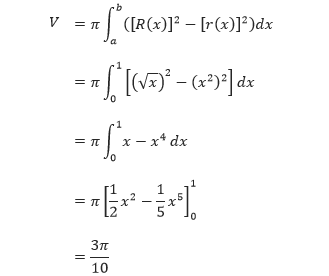
Apabila suatu luasan diputar pada sumbu tertentu, akan terbentuk suatu benda putar dengan volume sebesar luasan itu dikali dengan keliling putaran.

Dikarenakan keliling lingkaran adalah 2πr. Apabila luas bidang yang diputar = A, maka volume yaitu 2πr × A dipakai apabila batang potongan sejajar dengan sumbu putar.

Contoh Soal

1. Berapakah volume benda putar yang terbentuk dari daerah yang dibatasi kurva y = x2, sumbu x, dan 0 ≤ x ≤ 2 apabila diputar kepada sumbu x?

Jawab :

Metode cakram

Contoh Soal 2

Berapakah volume dari benda putar apabila daerah dibatasai oleh fungsi f(x) = 4 -x2. sumbu x, Dan sumbu y diputar 360º. Terhadap sumbu x dan terhadap sumbu y ?

a. Diputar mengelilingi sumbu x

Maka dari grafik di tersebut terlihat bahwa luasan r dibatasi titik di sumbu x (0,0) dan juga (0,2).

Sehingga, volume benda putar apabila luasan M diputar mengelilingi sumbu x ialah yaitu sebesar 360º = 256/15 π.

b. Diputar mengelilingi sumbu y

Mencari volume benda putarnya yang harus menyatakan kurva y = f(x) = 4-x2 untuk menjadi bentuk persamaan x2.

y = 4-x2
x2 = 4-y

Sehingga luasan M memotong sumbu y pada titik (0,0) dan (0,4).

Sehingga, apabila M diputar 360º derajat mengelilingi sumbunya. Mampu menghasilkan volume 8 π satuan volume.