PERTEMUAN 16 (VOLUME BIDANG PUTAR DENGAN METODE CAKRAM)

VOLUME BIDANG PUTAR DENGAN

METODE CAKRAM

Volume Benda Putar – volume yang dihasilkan dari sebuah luasan yang diputar dengan poros putar tertentu (sumbu x / sumbu y). Salah satu bentuk pengaplikasian integral selain menghitung luas di bawah kurva juga untuk menghitung volume pada benda putar. Contoh paling sederhana dari benda putar yaitu tabung. Volume sebuah tabung didapatkan dari luas alas berbentuk lingkaran yang dikalikan tinggi.

Volume Benda Putar

Jika alas tabung yang dinyatakan dengan fungsi A(x) dan tinggi dari benda putar itu adalah panjang selang dari titik a ke b pada sumbu x atau y maka volume benda putar itu bisa dihitung dengan memakai rumus

Untuk mencari volume sebuah benda putar yang didapatkan dari sebuah luasan yang diputar menurut sumbu x dan y bisa memakai cara seperti penjelasan dibawah ini

Rumus Volume Benda Berputar

a. Volume Benda Putar Sumbu x yang dibatasi 1 Kurva

perhatikan gambar di atas.
Luasan di bawah kurva y=f(x) jika diputar dengan sumbu putar dengan titik batas a dan b mampu menghasilkan sebuah silinder tinggi selisih b dan a. Volume benda putar menurut sumbu x diatas bisa dicari memakai rumus

b. Volume Benda Putar Sumbu y yang dibatasi 1 Kurva

Volume benda putar dengan sumbu putar yaitu sumbu y, harus mengubah persamaan grafik yang awalnya y yang merupakan fungsi dari x menjadi kebalikannya yaitu x menjadi fungsi dari y.

y = f(x) menjadi x = f(y).

Contoh :
y = x2
x = √y

Setelah persamaan diubah, masukkan ke rumus:

Metode Menghitung Volume Benda Putar

Metode yang dipakai untuk menghitung volume benda putar memakai 2 integral yaitu :

1. Metode Cakram

Berdasarkan rumus Volume = Luas Alas . tinggi
Luas Alas selalu merupakan lingkaran maka Luas Alas = πr2 (r = jari jari putaran)
dipakai jika batang potongan tegak lurus dengan sumbu putar

Apabila suatu daerah pada bidang diputar menurut garis tertentu, maka akan menghasilkan benda ruang, dan garis tersebut disebut sebagai pusat putaran. Benda ruang hasil putaran yang paling sederhana adalah tabung tegak atau bisa kita sebut sebagai cakram, yang dapat dibentuk dengan memutar persegi panjang menurut suatu garis yang berimpit dengan salah satu sisinya, seperti yang terlihat pada gambar berikut.

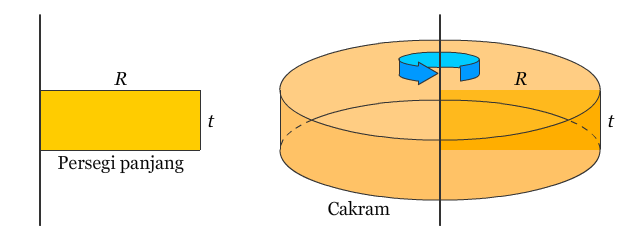
Sehingga, volume dari cakram tersebut dapat ditentukan sebagai berikut.

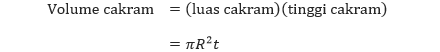
Dengan R dan t secara berturut-turut adalah jari-jari dan tinggi cakram.

Untuk melihat bagaimana penggunaan volume cakram dalam menentukan volume benda putar yang lebih umum, perhatikan gambar berikut.

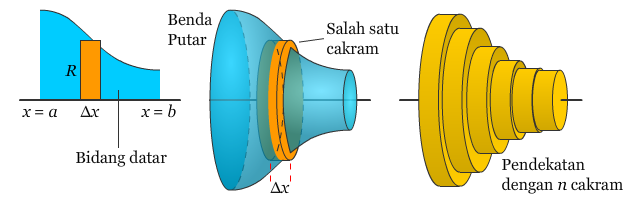
Untuk menentukan volume benda putar, perhatikan persegi panjang yang terletak pada bidang datar. Apabila persegi panjang tersebut diputar dengan pusat pada suatu garis, akan terbentuk salah satu cakram dalam benda putar yang volumenya,

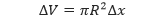
Sehingga volume benda putar tersebut dapat didekati dengan menggunakan n buah cakram yang memiliki tinggi Δx dan jari-jari R(xi) yang menghasilkan,

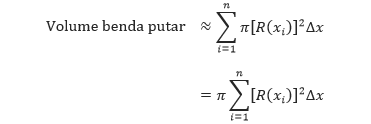
Pendekatan volume benda putar tersebut akan semakin baik apabila banyak cakramnya mendekati tak hingga, n → ∞ atau ||Δ|| → 0. Sehingga, kita dapat mendefinisikan volume benda putar sebagai berikut.

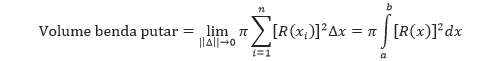
Secara sistematis, menentukan volume benda putar dengan metode cakram dapat dilihat seperti berikut.

Rumus yang serupa juga dapat diturunkan apabila sumbu putarannya vertikal. Apabila sumbu putarannya adalah vertikal (sumbu-y), maka rumus volume benda putarnya adalah sebagai berikut.

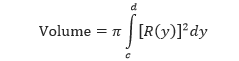
Untuk membedakan antara volume benda putar dengan pusat di garis horizontal ataupun vertikal, perhatikan gambar berikut.

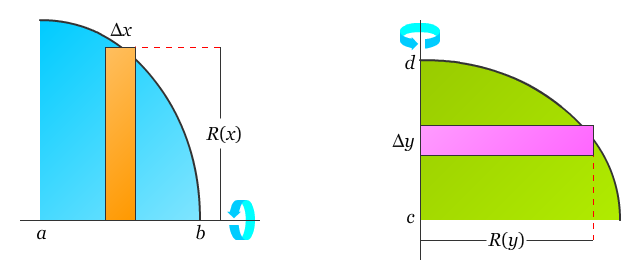
Aplikasi paling sederhana dari metode cakram adalah menentukan volume benda putar hasil putaran daerah yang dibatasi oleh grafik fungsi f dan sumbu-x. Jika sumbu putarannya adalah sumbu-x, maka dengan mudah dapat ditentukan bahwa R(x) sama dengan f(x). Perhatikan contoh berikut.

Contoh: Penggunaan Metode Cakram

Tentukan volume bangun ruang yang dibentuk oleh perputaran daerah yang dibatasi oleh grafik,

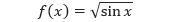
Dan sumbu-x (0 ≤ x ≤ π) dengan pusat putaran sumbu-x.

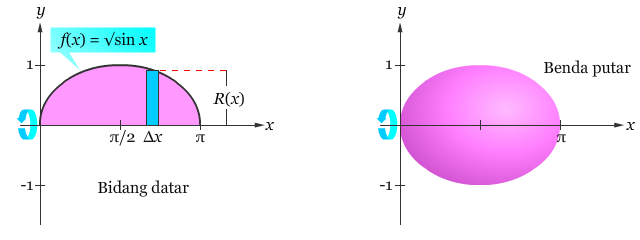
Pembahasan Dari persegi panjang biru di atas, dengan mudah kita dapat memperoleh jari-jari dari bangun ruang adalah,

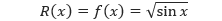
Sehingga volume dari benda putar yang terbentuk dapat ditentukan sebagai berikut.

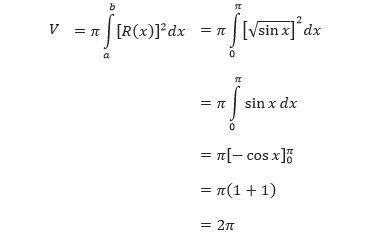
Jadi, volume benda putar yang terbentuk adalah 2π satuan volume.

2. Metode Cincin Silinder

Jika suatu luasan diputar pada sumbu tertentu, akan terbentuk suatu benda putar dengan volume sebesar luasan itu dikali dengan keliling putaran.
Dikarenakan keliling lingkaran adalah 2πr, jika luas bidang yang diputar = A, maka volume adalah 2πr × A
dipakai jika batang potongan sejajar dengan sumbu putar