PERTEMUAN 17 (VOLUME BIDANG PUTAR DENGAN METODE KULIT TABUNG)

VOLUME BIDANG PUTAR DENGAN METODE KULIT TABUNG


Untuk menentukan volume benda putar dengan integral bisa digunakan 2 metode atau cara. Metode tersebut adalah metode cakram  dan metode kulit tabung. Menambahkan pilihan dari metode sebelumnya, pada halaman ini akan diuraikan bagaimana cara menghitung volume benda putar dengan metode Kulit Tabung.

METODE KULIT TABUNG
Untuk menentukan volume benda putar dengan metode kulit tabung, gunakan salah satu dari rumus berikut, seperti yang ditunjukkan oleh gambar di bawahnya.
Sumbu putarnya horizontal,
Sumbu Putar Horizontal
Sumbu putarnya vertikal,
Sumbu Putar Vertikal

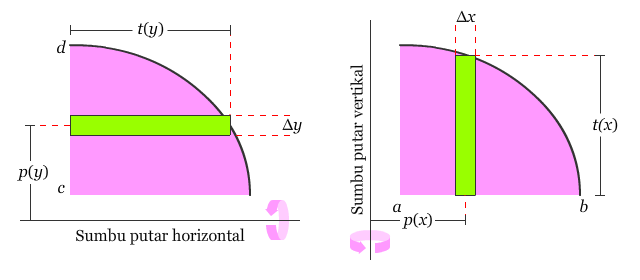
Metode Kulit Tabung

Untuk lebih memahami dalam menentukan volume benda putar dengan menggunakan metode kulit tabung, perhatikan beberapa contoh berikut.

Contoh I: Penggunaan Metode Kulit Tabung untuk Menentukan Volume

Tentukan volume benda putar yang dibentuk oleh putaran daerah yang dibatasi oleh

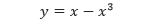
Fungsi Contoh Soal I

dan sumbu-x (0 ≤ x ≤ 1) dengan sumbu putarannya adalah sumbu-y.

Pembahasan Karena sumbu putarannya vertikal, gunakan persegi panjang vertikal, seperti yang ditunjukkan oleh gambar di bawah.

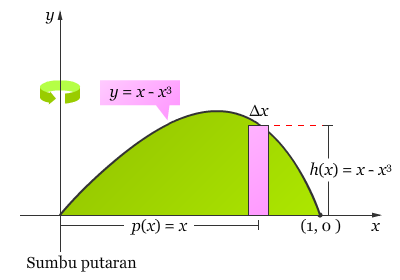
Contoh Soal I

Ketebalan Δx mengindikasikan bahwa x merupakan variabel dalam proses integrasi yang akan dilakukan. Jarak antara pusat persegi panjang dengan sumbu putaran adalah p(x) = x, dan tingginya adalah

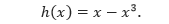
Tinggi Contoh Soal I

Karena rangenya antara 0 sampai 1, maka volume benda putar yang terbentuk dapat ditentukan sebagai berikut.

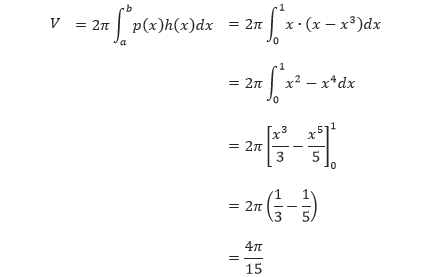
Pembahasan Contoh Soal I

Contoh II: Penggunaan Metode Kulit Tabung untuk Menentukan Volume

Tentukan volume benda putar yang dibentuk oleh putaran daerah yang dibatasi oleh

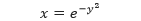
Fungsi Contoh Soal II

dan sumbu-y (0 ≤ y ≤ 1) dengan sumbu-x sebagai sumbu putarnya.

Pembahasan Karena sumbu putarannya horizontal, gunakanlah persegi panjang horizontal, seperti yang ditunjukkan gambar di bawah ini.

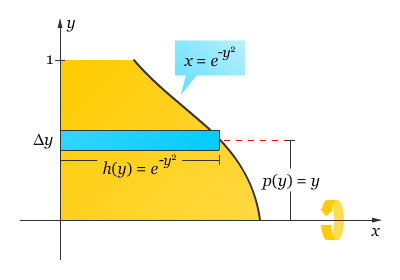
Contoh Soal II

Jarak antara pusat persegi panjang dan sumbu putarannya adalah p(y) = y, dan panjang dari persegi panjangnya adalah

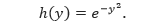
Tinggi Contoh Soal II

Karena range dari y dari 0 sampai 1, maka volume benda putarnya dapat ditentukan sebagai berikut.

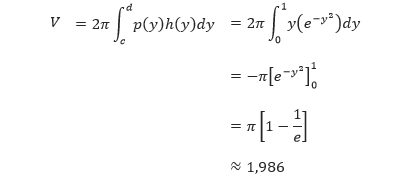
Pembahasan Contoh Soal II

Metode kulit tabung secara matematis dapat diilustrasikan sebagaimana gambar di bawah.







Secara umum apabila daerah yang dibatasi oleh kurva y=f(x) dan y=g(x) dengan |f(x)| > |g(x)| pada interval [a, b] diputar mengelilingi sumbu-X, maka volume benda putar yang diperoleh dapat ditentukan dengan menggunakan integral tentu sebagai berikut:

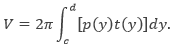
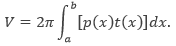
Komentar

Posting Komentar

Postingan populer dari blog ini

PERTEMUAN 18 ( VOLUME BIDANG PUTAR DENGAN METODE CINCIN )

Gambar
VOLUME BIDANG PUTAR DENGAN METODE CINCIN Volume Benda Putar merupakan sebuah volume yang dihasilkan dari luasan yang diputar dengan poros putar tertentu (sumbu x / sumbu y). Jadi salah satu bentuk pengaplikasian integral. Selain untuk menghitung luas di bawah kurva juga untuk menghitung volume pada benda putar. Misal paling sederhana dari benda putar adalah tabung. Volume sebuah tabung tersebut didapatkan dari luas alas yang memiliki bentuk lingkaran yang dikalikan tinggi. metode cincin ( washer method ), yaitu suatu metode yang menggunakan integral dalam menentukan volume benda putar yang memiliki lubang. Cincin dalam metode ini dibentuk oleh hasil putaran persegi panjang terhadap sumbu putaran tertentu (sumbu putaran tidak berimpit dengan sisi persegi panjang), seperti terlihat pada gambar berikut. Jika  r  dan  R  secara berturut-turut merupakan jari-jari dalam dan luar dari cincin dan  t  merupakan ketebalan cincin, maka volumenya dapat ditentukan sebag...
Baca selengkapnya

PERTEMUAN 16 (VOLUME BIDANG PUTAR DENGAN METODE CAKRAM)

Gambar
VOLUME BIDANG PUTAR DENGAN METODE CAKRAM Volume Benda Putar –  volume yang dihasilkan dari sebuah luasan yang diputar dengan poros putar tertentu (sumbu x / sumbu y). Salah satu bentuk pengaplikasian integral selain menghitung luas di bawah kurva juga untuk menghitung volume pada benda putar. Contoh paling sederhana dari benda putar yaitu tabung. Volume sebuah tabung didapatkan dari luas alas berbentuk lingkaran yang dikalikan tinggi. Volume Benda Putar Jika alas tabung yang dinyatakan dengan fungsi A(x) dan tinggi dari benda putar itu adalah panjang selang dari titik a ke b pada sumbu x atau y maka volume benda putar itu bisa dihitung dengan memakai rumus Untuk mencari volume sebuah benda putar yang didapatkan dari sebuah luasan yang diputar menurut sumbu x dan y bisa memakai cara seperti penjelasan dibawah ini Rumus Volume Benda Berputar a. Volume Benda Putar Sumbu x yang dibatasi 1 Kurva perhatikan gambar di atas. Luasan di bawah kurva y=f(x) jika diputar dengan sumbu putar deng...
Baca selengkapnya